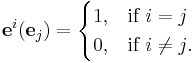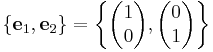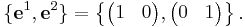Dual basis

In linear algebra, a dual basis is a set of vectors that forms a basis for the dual space of a vector space. For a finite dimensional vector space V, the dual space V* is isomorphic to V, and for any given set of basis vectors {e₁, …, e_n} of V, there is an associated dual basis {e¹, …, eⁿ} of V* with the relation

$\mathbf{e}^i (\mathbf{e}_j) = \begin{cases} 1, & \text{if } i = j \\ 0, & \text{if } i \ne j\text{.} \end{cases}$

Concretely, we can write vectors in an n-dimensional vector space V as n×1 column matrices and elements of the dual space V* as 1×n row matrices that act as linear functionals by left matrix multiplication.

For example, the standard basis vectors of R² (the Cartesian plane) are

$\{\mathbf{e}_1, \mathbf{e}_2\} = \left\{ \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right\}$

and the standard basis vectors of its dual space R²* are

$\{\mathbf{e}^1, \mathbf{e}^2\} = \left\{ \begin{pmatrix} 1 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 \end{pmatrix} \right\}\text{.}$

In 3-dimensional space, for a given basis {e₁, e₂, e₃}, you can find the biorthogonal (dual) basis by these formulas:

$\mathbf{e}^1=\frac{\left[\mathbf{e}_2;\mathbf{e}_3\right]}{\left(\mathbf{e}_1;\mathbf{e}_2;\mathbf{e}_3\right)}, \mathbf{e}^2=\frac{\left[\mathbf{e}_3;\mathbf{e}_1\right]}{\left(\mathbf{e}_1;\mathbf{e}_2;\mathbf{e}_3\right)}, \mathbf{e}^3=\frac{\left[\mathbf{e}_1;\mathbf{e}_2\right]}{\left(\mathbf{e}_1;\mathbf{e}_2;\mathbf{e}_3\right)}\text{.}$

In the above, the superscripts of the dual basis elements are indices.